Ir al contenido principal

Buscar este blog

Bioestadística #ULA

Facultad de Medicina, Universidad de Los Andes, Mérida, Venezuela

Facilitador Joan Fernando Chipia Lobo.

Entradas

Mostrando entradas de 2012

diciembre 22, 2012

Diagrama de Venn

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

diciembre 06, 2012

Teoría de conjuntos

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

noviembre 22, 2012

Técnicas de conteo

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

noviembre 15, 2012

Experimentos aleatorios, espacio muestral y eventos

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

noviembre 13, 2012

Las leyes del azar

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

noviembre 09, 2012

Probabilidad básica

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

noviembre 05, 2012

Cuentos para pensar

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

octubre 22, 2012

Contenidos a evaluar en el segundo parcial de Bioestadística

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

octubre 15, 2012

Micro Institucional de la Universidad de Los Andes

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

octubre 12, 2012

Medidas de Forma

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

septiembre 27, 2012

Bioestadística hasta el II parcial

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

septiembre 19, 2012

Presentación de Bioestadística ULA

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

septiembre 17, 2012

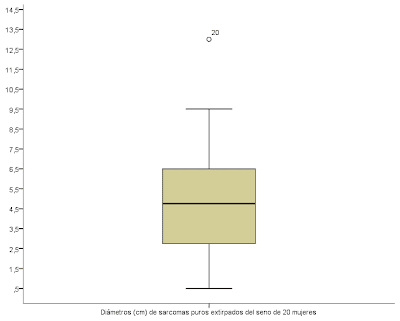
Gráficas de Caja

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

septiembre 03, 2012

Diagrama de tallos y hojas

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

agosto 29, 2012

Estadísticas vitales

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 21, 2012

Medidas de tendencia no central

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 20, 2012

Medidas de tendencia central

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 15, 2012

Índice de Masa Corporal

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 13, 2012

Resultados preliminares del Censo 2011

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

agosto 10, 2012

Técnicas e instrumentos de recolección de datos

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 09, 2012

Errores de medición

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 08, 2012

Planificación y ejecución de investigaciones médicas

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 07, 2012

Muestreo y sus tipos

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 02, 2012

Escalas de medición y variables estadísticas

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

agosto 01, 2012

Reseña histórica y conceptos básicos de Estadística

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Actitudes populares hacia la Estadística

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Indicador de salud

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

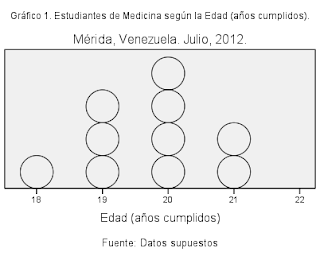
Gráfico de puntos y pictogramas

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Proporción, razón y tasa.

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Agrupamiento de datos cuantitativos

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Independencia de Venezuela

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Sesgos

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Escala tipo Lickert

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Validación de instrumentos

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Fechas importantes (U-2012)

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Calidad de la información

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Instrumentos de medición

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Nueva información (U-2012)

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Precisión y Exactitud

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Información (U-2012)

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Unidades de muestreo

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Tipos de muestreo

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Noticias estadísticas

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Estadísticas de Internet 2010

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Escalas de medición

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Santiago Ramón y Cajal

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Estadístico y Parámetro

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Información importante... (U-2012)

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Curiosidades estadísticas

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Sobre el Grupo (U-2012)

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Población, muestra y muestreo

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Importancia de la información estadística

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

El lenguaje de toma de decisiones en Estadística

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Introducción a la Bioestadística

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Blog de Bioestadística

Obtener enlace
Facebook
X
Pinterest
Correo electrónico
Otras aplicaciones

Publicar un comentario

Entradas más recientes Inicio

Con la tecnología de Blogger

Imágenes del tema: pixhook

Archivo del Blog

2024 13
- noviembre 2
- octubre 1
- septiembre 2
- agosto 1
- julio 1
- junio 1
- mayo 1
- abril 1
- marzo 1
- enero 2

2023 15
- octubre 2
- septiembre 1
- agosto 1
- julio 2
- junio 3
- mayo 1
- abril 2
- marzo 1
- febrero 1
- enero 1
2022 11
- noviembre 2
- octubre 2
- septiembre 1
- julio 2
- junio 1
- marzo 1
- enero 2
2021 4
- abril 1
- marzo 1
- febrero 1
- enero 1
2020 15
- diciembre 1
- noviembre 1
- agosto 1
- julio 1
- junio 1
- mayo 3
- abril 1
- marzo 2
- febrero 2
- enero 2
2019 3
2018 7
- diciembre 2
- octubre 1
- junio 1
- abril 1
- febrero 1
- enero 1
2017 7
- diciembre 1
- noviembre 1
- octubre 1
- mayo 1
- abril 1
- marzo 2
2016 9
- diciembre 1
- noviembre 1
- octubre 1
- junio 2
- mayo 1
- abril 1
- marzo 1
- febrero 1
2015 21
- noviembre 3
- octubre 6
- septiembre 1
- agosto 1
- julio 2
- junio 1
- mayo 2
- abril 1
- marzo 2
- febrero 1
- enero 1
2014 44
- diciembre 8
- noviembre 2
- octubre 2
- septiembre 2
- agosto 8
- julio 3
- junio 2
- mayo 2
- abril 2
- marzo 4
- febrero 6
- enero 3
2013 56
- diciembre 16
- noviembre 5
- octubre 6
- septiembre 2
- agosto 7
- julio 1
- junio 2
- mayo 4
- abril 7
- marzo 2
- febrero 2
- enero 2
2012 55

Mostrar más Mostrar menos

Etiquetas

Aprendizaje28
Base de Datos2
Big data1
Bioestadística76
Blog5
causalidad2
Censo2
Ciencia5
Combinaciones1
Conceptos básicos2

Mostrar más Mostrar menos

Denunciar abuso