Gráficas de Caja

La gráfica de caja es una representación que describe simultáneamente varias características importantes de un conjunto de datos, tales como el centro, la dispersión, la desviación de la simetría y la identificación de observaciones que caen inusualmente lejos de la mayoría de datos (a estas observaciones se le llaman valores atípicos).

En este tipo de gráfica se representan los tres cuartiles y los valores extremos (máximo y mínimo) en una caja rectangular alineada en sentido horizontal o vertical, abarcando el rango intercuartílico, con el borde izquierdo (o el inferior) de la caja el primer cuartil (Q1=P25) y en el borde derecho (o el superior) el tercer cuartil (Q3=P75). Se traza una línea a través de la caja en el segundo cuartil (Q2=D5=P50=Mediana). Posteriormente se traza una línea o bigote, desde cada extremo de la caja.

El bigote inferior o izquierdo es una línea que va desde el primer cuartil al punto correspondiente al menor de los datos dentro de 1,5 rangos intercuartílicos a partir del primer cuartil. El bigote superior o derechos  es una línea que va desde el tercer cuartil al punto correspondiente al mayor de los datos dentro de 1,5 rangos intercuartílicos a partir del tercer cuartil. Los datos que se encuentran alejados de la caja más allá de los bigotes se grafican como puntos individuales. A un punto situado después de un bigote, pero a menos de 3 rangos intercuartílicos de los bordes de la caja se le llama punto atípico, mientras que a un punto que se encuentre situado a más de 3 rangos intercuartílicos de los bordes de la caja se le denomina punto atípico extremo.

Ejemplo:

Daniel (2010) menciona que en la Revista American Journal of Clinical Pathology, Pitts y otros, asegura que "los carcinomas con metaplasia y sarcomas producidos dentro del seno son difíciles de diagnosticar y clasificar con precisión debido a sus variados patrones histológicos y a su rareza". En un intento por estudiar más detalles de las características biológicas, los autores investigaron una serie de sarcomas puros y carcinomas que exhibían metaplasia, a continuación se muestran los datos para la construcción de la gráfica de caja.

Diámetros (cm) de sarcomas puros extirpados de los senos de 20 mujeres.

0,5	1,2	2,1	2,5	2,5	3,0	3,8	4,0	4,2	4,5
5,0	5,0	5,0	5,0	6,0	6,5	7,0	8,0	9,5	13,0

Construcción de la gráfica:
Se calculan los cuartiles en el programa SPSS para Windows versión 19, se hace clic en el menú Analizar, se selecciona Estadísticos descriptivos y luego Frecuencias; en el cuadro diálogo que arroja se selecciona la variable en estudio, se hace clic en el botón Estadísticos... (ubicado en la parte superior derecha), se selecciona Cuartiles (ubicado en la parte superior izquierda), se hace clic en el botón Continuar y finalmente en Aceptar.

Los resultados obtenidos fueron los siguientes:

Q1=2,625 cm

Q2=4,75 cm

Q3=6,5 cm

Se calcula la Rango intercuartilar (RQ):

RQ = Q3 - Q1= 6,5 cm - 2,625 cm = 3,875 cm

El bigote superior va a quedar determinado por el mayor de los datos comprendidos entre  Q3 y Q3 + 1,5.RQ. Entonces se tiene que:

Q3 + 1,5.RQ = 6,5 cm + 1,5 (3,875 cm) = 6,5 cm + 5,8125 cm = 12,3125 cm

Por lo tanto el bigote superior llegará hasta el mayor de los datos entre 6,5 cm y 12,3125 cm, el cual es 9,5 cm.

El bigote inferior va a quedar determinado por el menor de los datos comprendidos entre  Q1 y Q1 - 1,5.RQ. Entonces se tiene que:

Q1 - 1,5.RQ = 2,625 cm - 1,5 (3,875 cm) = 2,625 cm - 5,8125 cm = -3,1875 cm

Por lo tanto el bigote inferior llegará hasta el menor de los datos entre 2,625 cm y -3,1875 cm, el cual es 0,5 cm.

También se tiene que el sarcoma de 13 cm de diámetro es un valor o punto atípico.

Para hallar esta gráfica en el paquete estadístico SPSS para Windows versión 19, se realiza el siguiente procedimiento:

Se hace clic en el menú Gráficos, se selecciona Cuadro de diálogos antiguos y luego Diagramas de caja...; en el cuadro diálogo que arroja se selecciona el Diagrama simple y Resúmenes para distintas variables, se hace clic en el botón Definir, se coloca la variable en estudio en el recuadro Las cajas representan y finalmente se hace clic en el botón Aceptar.

El resultado es el siguiente luego de la edición de escala:

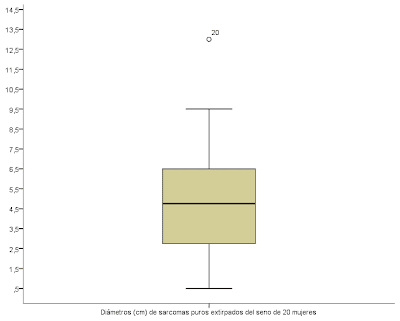
Gráfico 1. Diámetros (cm) de sarcomas puros extirpados de los senos de 20 mujeres.

Fuente: Daniel (2010).

Al examinar la gráfica se puede ver que el 50% central se encuentra entre 2,6 y 6,5 cm, además se puede observar que la Mediana está cercana a 4,5 cm. La línea o bigote más alargada en la parte superior indica que la distribución de diámetros está inclinada hacia la derecha o es asimétrica positiva. Asimismo, se puede notar que el programa estadístico indica cual es el dato extremo con un circulo y dice cuál es el número del mismo en la base de datos.

La gráfica de caja con valores extremos, así como el diagrama de tallos y hojas, son ejemplos de lo que se conoce como análisis exploratorio de datos. Estas técnicas, se hicieron populares debido al resultado del trabajo de Tuckey, permiten que el investigador examine datos de manera que éstos revelen tendencias y relaciones, identifique características únicas del conjunto de datos y faciliten su descripción y resumen.

Referencias:

Daniel, W. (2010). Bioestadística. Base para el análisis de las ciencias de la salud (4a. Ed.). México: Limusa Wiley.

Montgomery, D. y Runger, G. (2008). Probabilidad y estadística aplicada a la ingeniería (2a. Ed.). México: Limusa Wiley.