Buscar este blog
Facultad de Medicina, Universidad de Los Andes, Mérida, Venezuela
Facilitador Joan Fernando Chipia Lobo.
Entradas
Mostrando entradas de septiembre, 2012
Bioestadística hasta el II parcial
- Obtener enlace
- Correo electrónico
- Otras aplicaciones
Presentación de Bioestadística ULA
- Obtener enlace
- Correo electrónico
- Otras aplicaciones
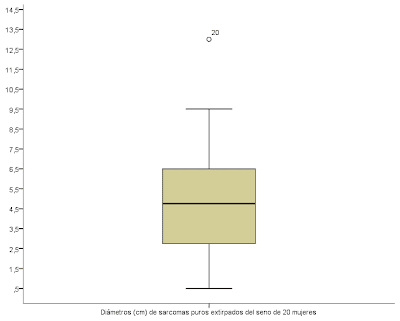
Gráficas de Caja
- Obtener enlace
- Correo electrónico
- Otras aplicaciones
Diagrama de tallos y hojas
- Obtener enlace
- Correo electrónico
- Otras aplicaciones